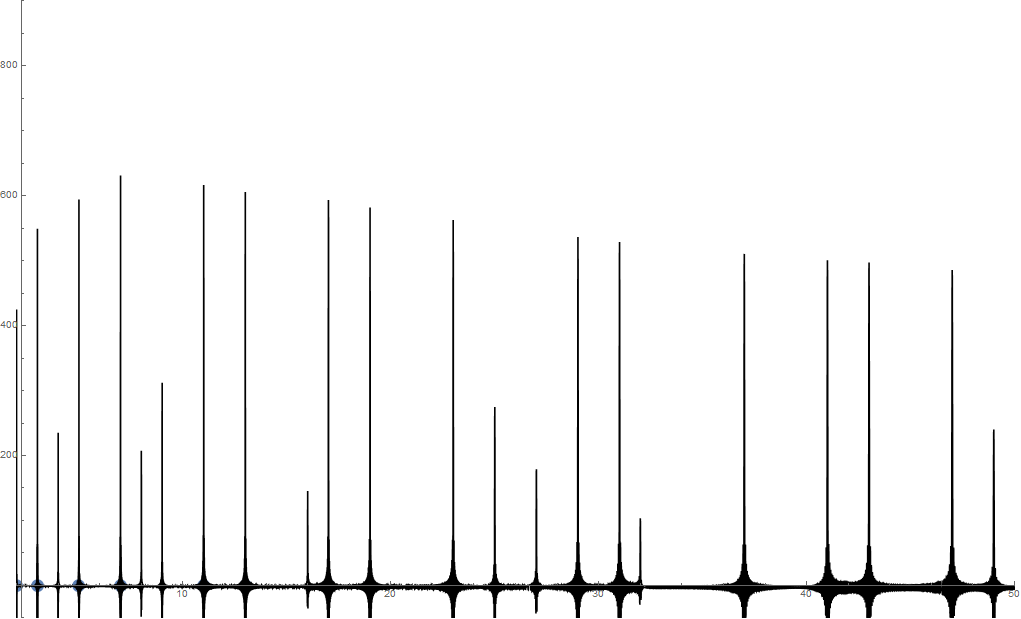
Die folgende Summenformel stellt das ‚Inverse Riemann-Spektrum‘ der nicht-trivialen Nullstellen der Zetafunktion dar. Sie zeigt beeindruckende Peaks bei den Positionen der Primzahlen und ihren Potenzen:
f(x)=-\sum _{n=1}^{\text{nmax}} \cos \left(\log (x) \Im\left(\rho _n\right)\right)
Hier geht die Summe über die Imaginärteile der nicht-trivialen Nullstellen der Riemannschen Zeta-Funktion und nimmt nmax Nullstellen. Je mehr Nullstellen für die Summation verwendet werden, desto stärker erscheinen die Peaks an Positionen von Primzahlen und Primzahlen-Potenzen. Die Höhe der Peaks, die zu einer Primzahl-Potenz n gehören, scheinen eine Länge von \frac{1}{n} der Länge des ursprünglichen Primzahl Peaks zu haben.
Wenn n gegen \infty geht, ähnelt die Funktion einer Art Delta-Funktion (bekannt aus der Physik). Wenn es einem genialen Mathematiker gelingen sollte, f(x) zu normalisieren und das Integral über diese Funktion zu berechnen, könnte man eine Formel für \pi (x) erhalten (streng genommen für die Funktion J(x), aber \pi (x) kann leicht von J(x) unter Verwendung der Moebius-Inversionsformel abgeleitet werden).
Hier ist ein Beispiel mit 500 Nullstellen mit einem Plot von f(x) im Bereich 2- 50. Zum Hinein-Zoomen bite auf die Grafik klicken:
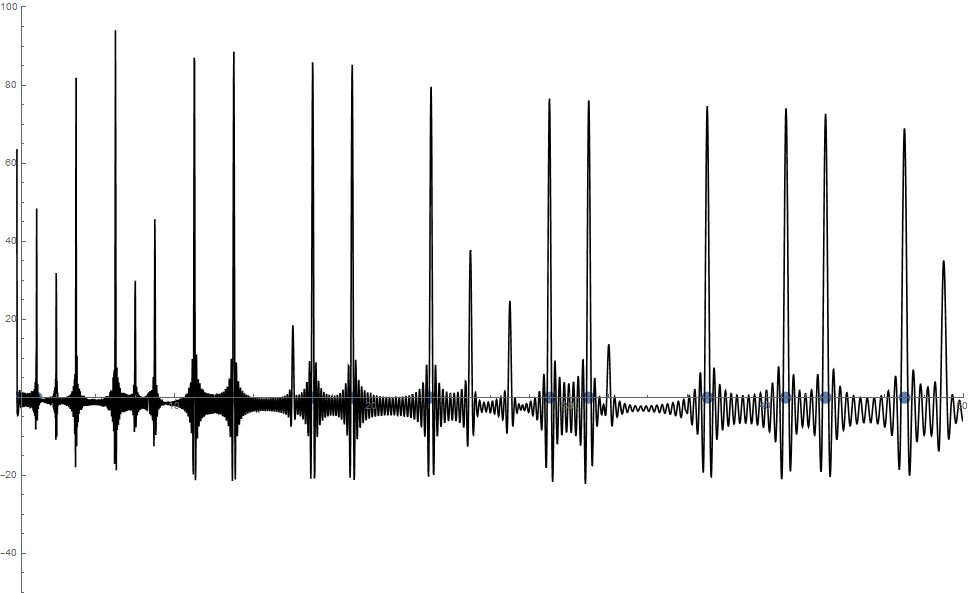
Hier ist ein Beispiel mit 1000 Nullstellen mit einem Plot von f(x) im Bereich 2- 50. Zum Hinein-Zoomen bite auf die Grafik klicken.
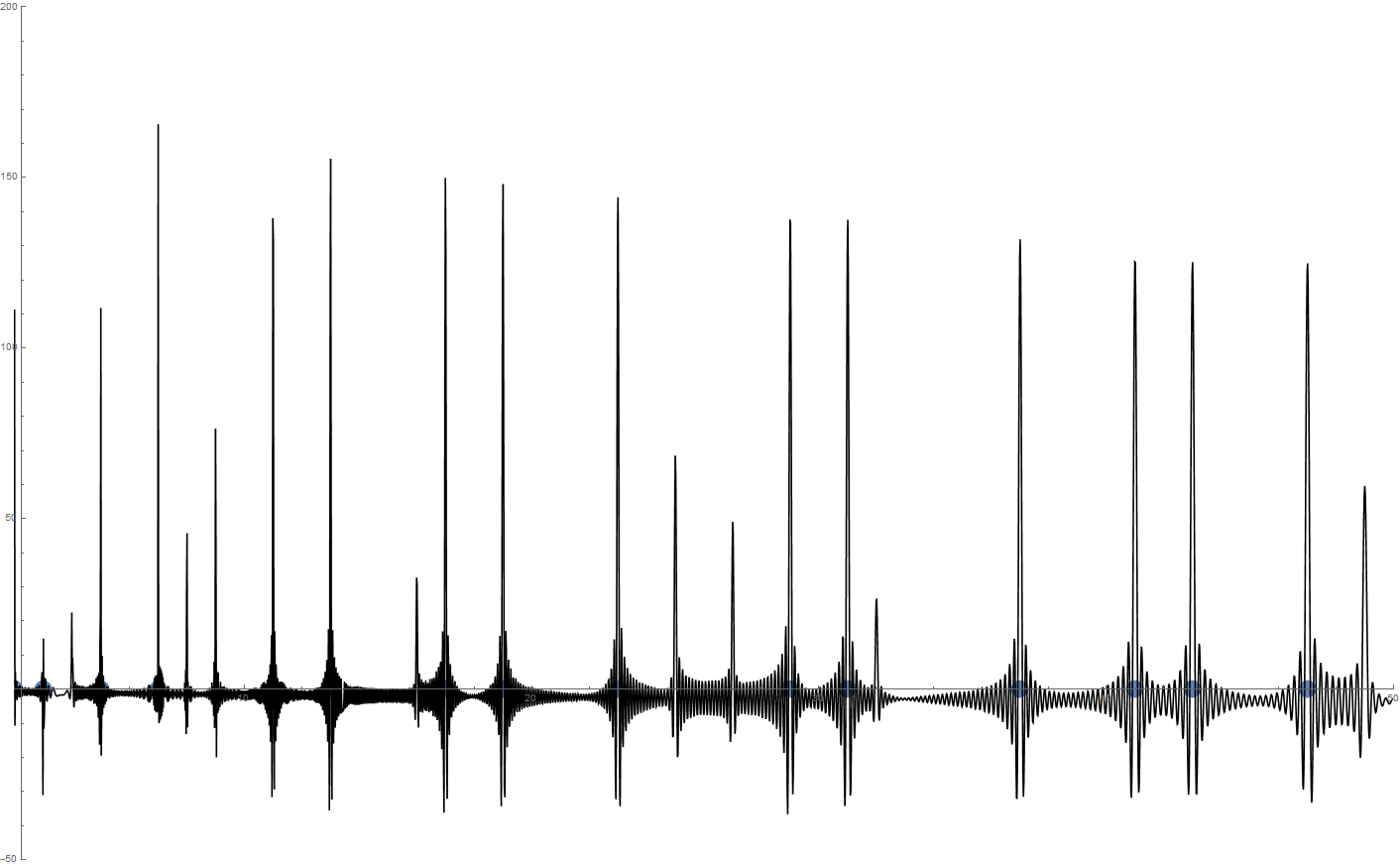
Hier ist ein Beispiel mit 5000 Nullstellen mit einem Plot von f(x) im Bereich 2- 50. Zum Hinein-Zoomen bite auf die Grafik klicken.