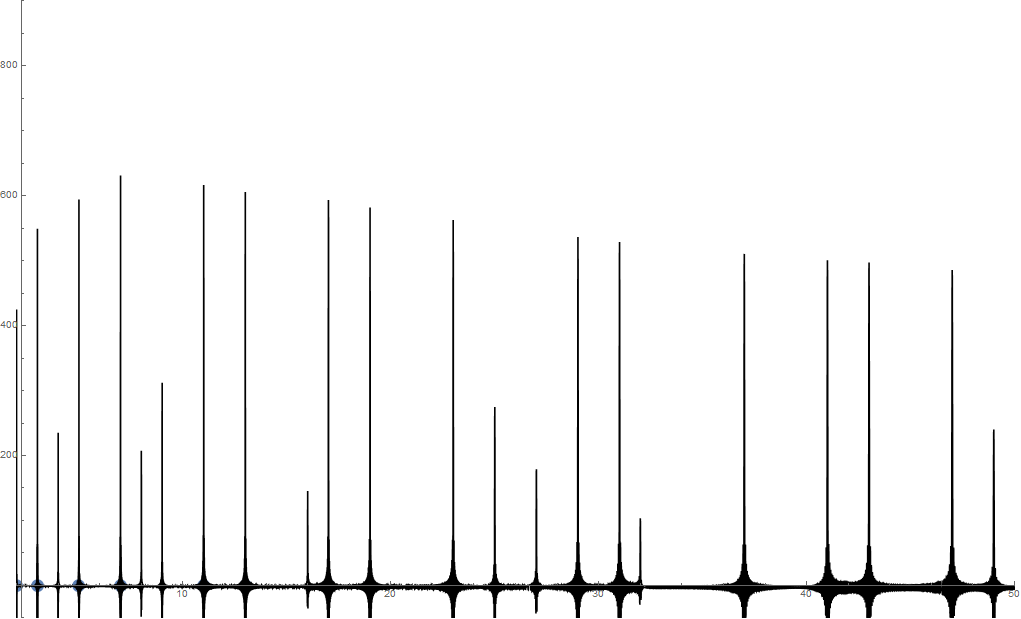
формулу суммы, которая показывает очень впечатляющие пики на позициях простых чисел и их степеней. Формула отличается простотой и элегантностью:
f(x)=-\sum _{n=1}^{\text{nmax}} \cos \left(\log (x) \Im\left(\rho _n\right)\right)
Здесь сумма идет по мнимым частям нетривиальных нулей дзета-функции Римана, принимая нули nmax. Чем больше нулей берется для суммирования, тем более острые пики появляются на позициях простых чисел и простых степеней. Длина пиков, принадлежащих основной мощности, по-видимому, имеет длину \frac{1}{n} исходного простого пика.
Для перехода в \infty функция похожа на своего рода Дельта-функцию (известную из физики). Если талантливый математик сумеет нормализации и построения интеграла Ф(Х) можно получить формулу для \pi (x) (строго говоря, для функции J(x), но \pi (x) можно легко вывести из J(x) , используя формулу инверсии Мебиуса)…
Вот пример с 500 корнями, построение f(x) в диапазоне 2 — 50. Пожалуйста, нажмите на изображение для увеличения:
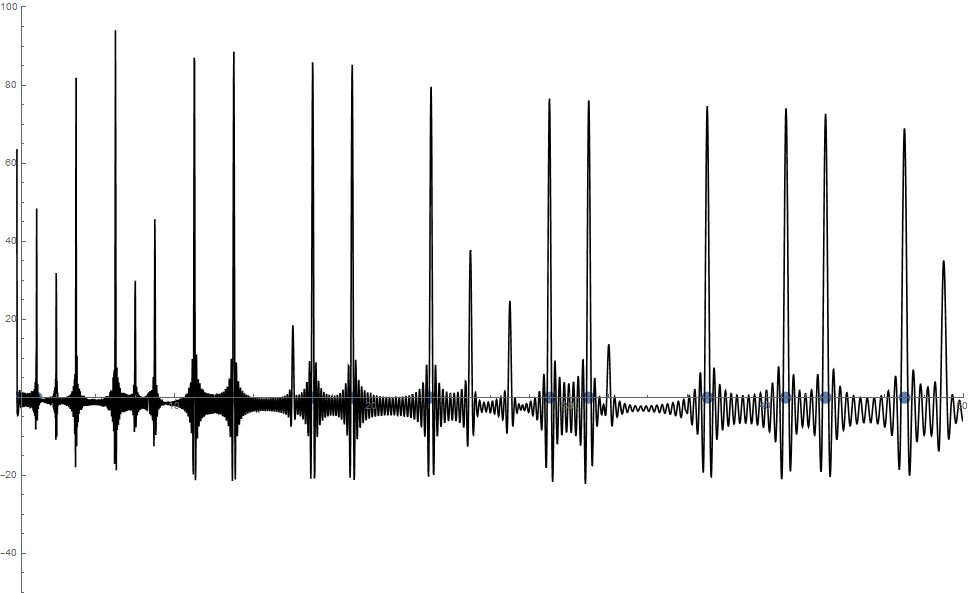
Вот пример с 1000 корнями, построение f(x) в диапазоне 2 — 50. Пожалуйста, нажмите на изображение для увеличения:
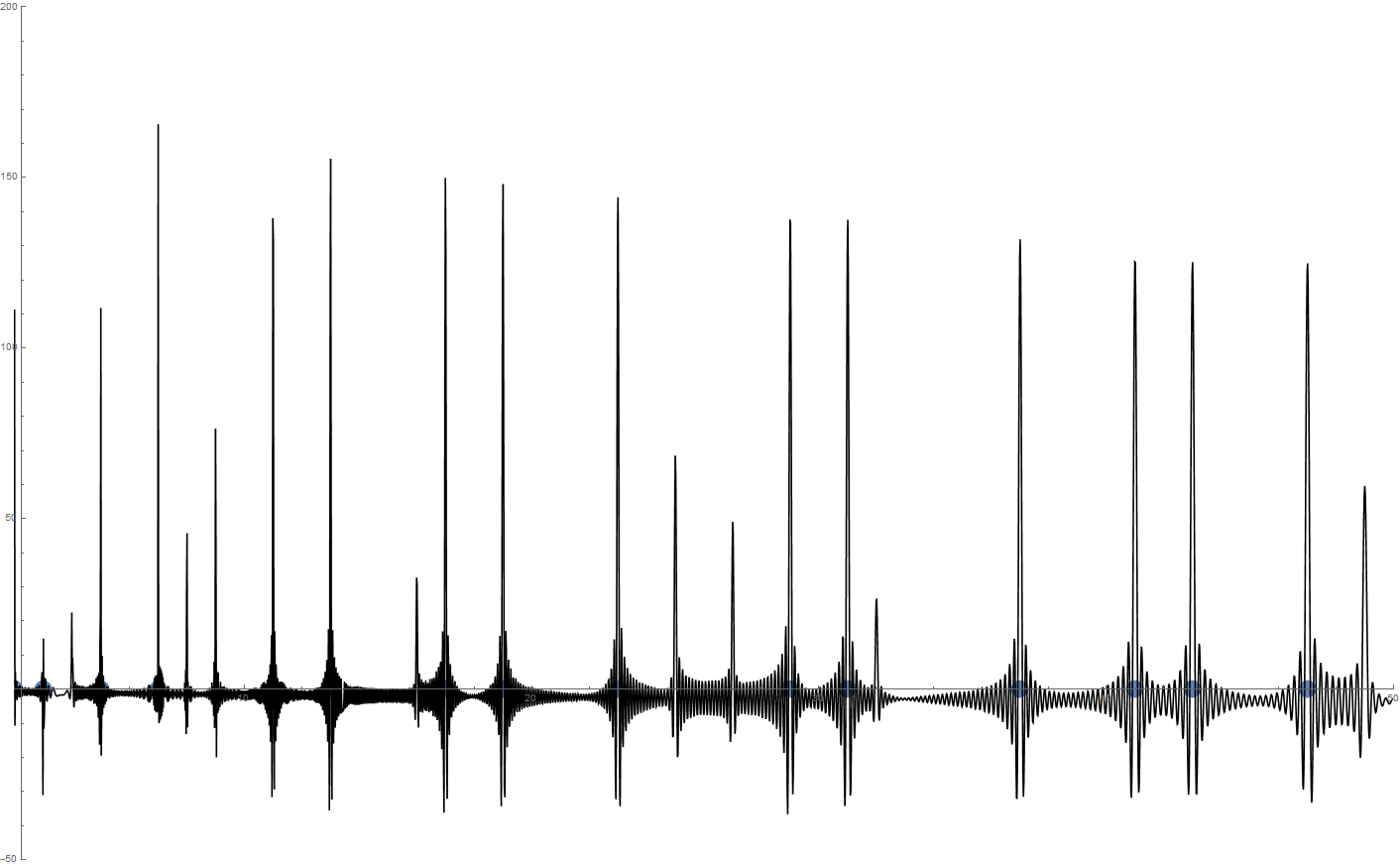
Вот пример с 5000 корнями, построение f(x) в диапазоне 2 — 50. Пожалуйста, нажмите на изображение для увеличения: