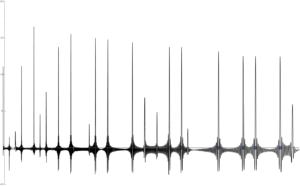
Peter Danzeglocke has come up with the following sum formula which shows very impressive peaks at the positions of primes and their powers. The formula stands out for its simplicity and elegance:
f(x)=-\sum _{n=1}^{\text{nmax}} \cos \left(\log (x) \Im\left(\rho _n\right)\right)
Here the sum goes over the imaginary parts of the non trivial zeros of Riemanns Zeta function, taking nmax zeros. The more zeros are taken for summation, the more sharp peaks appear at positions of primes and prime powers. The length of the peaks belonging to a prime power of n appear to have a length of \frac{1}{n} of the original prime peak.
For n going to \infty the function is similar to a kind of delta function (known from physics). If a gifted mathematician succeeds in normalizing and building the integral over f(x) one could get a formula for \pi (x) (strictly speaking for the function J(x), but \pi (x) can be easily derived from J(x) be using the Moebius inversion formula…
Here an example with 500 zeros, plotting f(x) in the range 2 – 50. Please click on the image for zooming in: